江西省公务员考试行测图形推理——数量型
发布时间：2015-04-05 11:48:58 来源：一佳公务员考试网 点击量：
│
在图形推理中，有很多图形中都隐含了基本的数量关系，就好比数字推理，需要考生根据已知的数字规律得出答案。按从大到小分类，数量型包括素、面、角、线、点五个方面的考查内容，其中素是指元素，如圆形、三角形、方形等，而面是指封闭面。具体的知识分类如下：
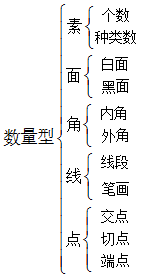下面通过具体的真题来讲解数量型的基本考法及对应的解题方法。
【例1】（2010年国考）
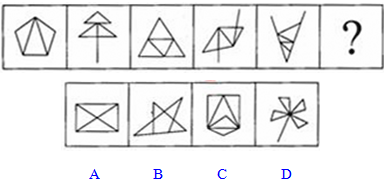
【一佳名师解析】此题答案为A。从整体上看，本题中最明显的特征就是三角形这个元素，它们的数量分别是3、4、5、6、7、？，呈现出明显的规律，所以接下来应是8个三角形，因此答案为A。
【变1】（2011年4•24联考）
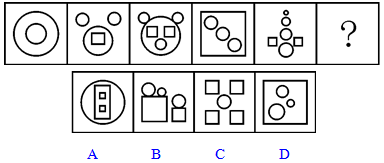
【一佳名师解析】此题答案为D。从整体上看，本题中最明显的特征就是含有圆和方两个基本元素，而且圆的个数明显都比方的个数要多，具体数一下是多2个，符合此规律的就是D项，因此答案为D。
核心提示：元素的个数一般可以重叠地数，只要数的元素不重复就可以了。
【例2】（2009年国考）
【一佳名师解析】此题答案为A。从第一、三、五个图来看，它们有两个共同的规律，那就是元素个数分别是2、3、4，元素种类数都是1；如果考虑元素的个数，那么第二、四个图都是有2个三角形，接下来应该也是2个相同元素，发现A、B、C都符合；于是考虑种类数，第二、四个图中都含有2种元素，接下来应该也是2种元素，发现只有A项符合，因此答案为A。
【变2】（2011年4•24联考）
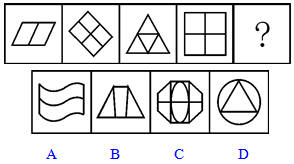
【一佳名师解析】此题答案为A。如果考虑元素个数，此题同样无解，于是我们可以考虑种类数，发现每一个图都含有1类元素，因此答案为A。
需要注意的是，按属性的“曲直性”规律，我们可以得到一个不同于A项的答案，即B项，理由是前面所有的图都是“直线图”，而选项中只有B项是“直线图”，因此B项是一个答案。这就出现了“按不同的规律得出来的答案不同”这样的问题，对于这种问题，考生应按“最优规律”来选，一般来说，数量上的规律是很难“偶然”得到的，这才是出题者真正的意图所在。
核心提示：“相同或相似的图形为一类图”，这是判断种类数的一般规律。对于连在一起的图形，判断种类数时应拆分开来看，即按公共边剪开后再按前面的规律判断种类数。
【例3】（2008年浙江）
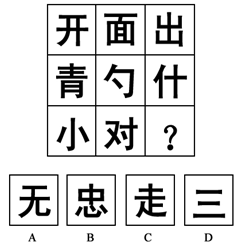
【一佳名师解析】此题答案为D。九宫格第一行的部分数都是1，第二行的部分数都是2，第三行前两个的部分数都是3，”？”处也应是3，因此答案为D。
【变3】（2011年4•24联考）
【一佳名师解析】此题答案为D。从整体上看，差不多每个图形组成都比较零散，很容易考虑到元素的个数（部分数），它们的个数分别是1、2、3、4、5、？，接下来应该是6，因此答案为D。
核心提示：在图形推理中，“连在一起的”就算一个部分。部分数可以归类为元素的个数。
【例4】（2009年国考）
【一佳名师解析】此题答案为C。从整体上看，有两类元素，而且在个数上存在变化，在第一组图中，圆的个数分别是4、2、0，五角星的个数分别是0、1、2，都是呈等差变化规律；同样，第二组图的圆的个数分别是4、2、？，五角星的个数分别是1、2、？，理应也呈等差变化规律，即有0个圆，3个五角星，因此答案为C。
实际上，此题存在着一种换算关系：一个五角星＝两个圆，于是，第一组都是4个圆，第二组都是6个圆，同样得出答案为C。
【变4】（2010年浙江）
【一佳名师解析】此题答案为A。如果考虑方向的话，此图中含有两类元素，一类是上三角，一类是下三角，而比较多的元素是下三角，所以我们希望能把前面的几个图都转变成下三角；由于第四个图有7个下三角，而第三个图只有2个上三角，所以不太可能是常数规律（因为都是7个下三角将不能按整数换算），考虑等差规律，而等差可能是递增的，也可能是递减的，需要试探：假设一个上三角＝三个下三角，那么换算结果是8、8、6、7，不成规律，因此考虑一个上三角＝四个下三角，那么换算结果是10、9、8、7，有规律，因此接下来应是6个下三角，因此答案为A。
核心提示：换算关系容易出现在图形中只含有两到三类元素的题目之中，而且元素的个数存在着一定的变化。换算关系一般不需要解方程，我们往往可以通过验证来得到答案，一般先按常数规律验证，否则按等差规律验证，一般把个数少的元素换成个数多的元素。
【例5】（2010年9•18联考）
【一佳名师解析】此题答案为C。从整体上看，图形中面的特征非常明显，于是考虑数封闭面的个数，发现它们都是4个，因此答案为C。
【变5】（2012年国考）
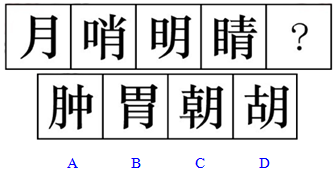
【一佳名师解析】此题答案为B。围绕汉字的考点很多，比如笔画数、部分数、封闭面数、结构关系和运算关系等，此题就是考查封闭面的个数，分别为2、3、4、5、？，接下来应该是6个封闭面，因此答案为B。
核心提示：封闭面一般是指“白面”，即那些被线段围成的空白面。
【例6】（2009年山东）
【一佳名师解析】此题答案为D。从整体上看，本题的图形中既有白面又有黑面，而且黑面的个数更少，分别是1、4、3、2、？，这是一个乱序数列，重新排列后“？”处应是5，即5个黑面，因此答案为D。
【变6】（2011年9•17联考）
【一佳名师解析】此题答案为B。在这种格状图中，有白格也有黑格，一般情况下我们优先考虑黑格，比如可以考虑黑格的个数，或黑格的移动等。此题中黑格个数变化比较大，优先去考虑它们的个数，即每一行的个数分别是2、4、4；4、4、6；6、2、？。初一看这些数字并没有什么规律，但整体上看，它们都是偶数，而奇偶性也是一个规律，选项中只有B项有偶数个黑格，因此答案为B。
核心提示：黑面个数的考查不多见，但考生还是要关注这个考点，看到黑白图形时可以从黑白两个方面进行思考。
【例7】（2009年4•26联考）
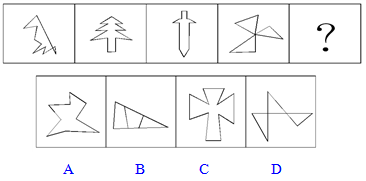
【一佳名师解析】此题答案为D。从整体上看，本题角的特征非常明显，于是考虑数角的个数，分别是9、9、9、9、？，显然，接下来也是9个角，因此答案为D。
【变7】（2010年江苏）
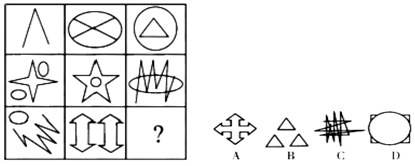
【一佳名师解析】此题答案为B。从整体上看，本题角的特征非常明显，优先考虑角的个数，前两行分别是1、4、3，4、5、6，发现只有一处不顺眼，即第一行第二个图，要是2的话，这个规律就自然了，再结合其他图角的特征，可以确定此题应是数“锐角”个数，于是”？”处应是9个锐角，毫无疑问答案是3个锐角三角形，因此答案为B。
核心提示：数角的时候需要注意，对于封闭图形来说，我们应该数“内角”，而对于非封闭图形来说，只要是一个角就要数。
【例8】（2010年4•25联考）
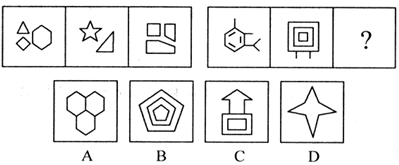
【一佳名师解析】此题答案为C。从整体上看，图形基本上都是多边形，考虑数边的个数，发现第一组图都是13条直线（段），第二组图的前两个图都是14条直线（段），于是“？”处也是14条直线（段），因此答案为C。
【变8】（2011年9•17联考）
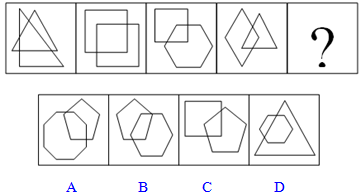
【一佳名师解析】此题答案为C。本题中的图形都是由多边形构成的，而且每个图中均含有两个多边形，它们之间有叠交的部分，考生应该把重点放在这些特殊的叠交部分，发现叠交部分都是四边形，因此答案为C。
核心提示：线段包括直线段和曲线段两种，如果线段数比较多，我们应该尽量做乘法，如本题中的选项A有3×6－3＝15条直线段，B有3×5＝15条直线段。
【例9】（2008年浙江）
【一佳名师解析】此题答案为C。从整体上看，本题中所有的图都是曲线图，应数曲线段的个数，分别是1、2、3、4、？，接着应该是5，因此答案为C。
【变9】（2010年浙江）
【一佳名师解析】此题答案为B。与上一题相比，本题更具迷惑性，基本特征是有直线，也有曲线，还有不同的元素，直线基本上没有什么规律，考虑曲线段的个数，分别是3、3、3、3，很明显，我们要找一个含有3条曲线段的图形，因此答案为B。
核心提示：一段完整的圆弧（包括封闭的圆）就算一个曲线段。
【例10】（2009年4•26联考）
【一佳名师解析】此题答案为C。从整体上看，本题中所有的图形都是连在一起的，即为一个部分，因此答案为C。
实际上，上面九宫格中所有的图形都能够一笔画，“一笔画问题”是近年来国考和联考中喜欢考到的一个问题，考生要能够快速进行判断，即什么样的图形可以一笔画，不管这个图形多么复杂。关于一笔画的判定，早在1736年，著名的数学家欧拉就提出了解决办法，简单地说，就是“奇点数是0或2的图形可以一笔画”。
【变10】（2011年9•17联考）
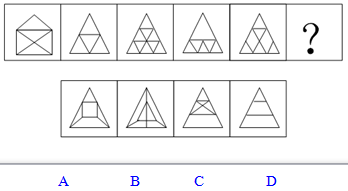
【一佳名师解析】此题答案为C。与上一题相比，本题更具有隐蔽性，考生一般会从直线段的个数或面的个数这些常规的方向思考，但是都不能得到答案，此时我们可以考虑一笔画的问题，根据一笔画的判定标准，前面所有的图形都可以一笔画，比如第一个图形的奇点数为2（底上的两个顶点），后三个图形奇点数均为0，第五个图形奇点数为2（腰上的两个点），它们都能一笔画，而选项中A有4个奇点，B有6个奇点，C有0个奇点，D有4个奇点，因此答案为C。
核心提示：图形中的点有两种，一种是奇点，一种是偶点，按点的发散方向来确定，即如果一个点有奇数个发散方向，则这个点就是奇点，如果有偶数个发散方向，则为偶点。
【例11】（2012年国考）
【一佳名师解析】此题答案为D。本题考生可能会先考虑封闭面的个数，但没有规律，注意到第一行图都是一笔画图，第二行中都是两笔画图，第三行中前两个都是三笔画图，所以“？”处也是三笔画图，因此答案为D。
【变11】（2012年浙江）
【一佳名师解析】此题答案为B。与上题类似，本题的第一行也是一笔画图，第二行是两笔画图，第三行是三笔画图，因此答案为B。
核心提示：此题考到“多笔画”问题，实际上，在前面一笔画问题的基础上再进一步，我们不可以得到多笔画问题的判定，即“奇点数的个数是2N的图形可以N笔画”。
【例12】（2010年北京）
【一佳名师解析】此题答案为B。汉字或字母的笔画数与前面所说的一笔画和多笔画是不同的，这里需要单独分开来，汉字或字母的笔画数就按我们书写的习惯来确定，如本题的笔画数分别是13、11、9，呈等差变化，接着应是7，因此答案为B。
【变12】（2011年北京）
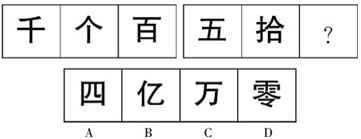
【一佳名师解析】此题答案为D。数一下汉字的笔画数，第一组分别是3、3、6，第二组分别是4、9、？，在第一组中，3＋3＝6，于是“？”处的笔画数为4＋9＝13，因此答案为D。
【例13】（2009年江苏）
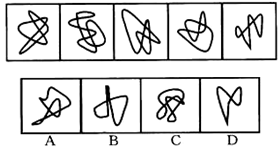
【一佳名师解析】此题答案为B。本题考生的第一印象可能是去数封闭面的个数，它们确实有规律，分别是8、7、6、5、4、？，接着应该是3，但扫描选项发现没有3个面的图，所以此题并不是要求大家去数面；除面的特征明显外，此题“相交”的特征也很明显，于是考虑数交点的个数，分别是7、6、5、4、3、？，接着应该是2，B就有2个交点，因此答案为B。
【变13】（2009年浙江）
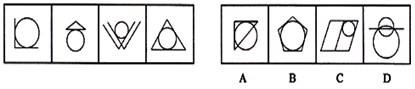
【一佳名师解析】此题答案为A。本题图形相切的特征比较明显，于是可以先考虑切点的个数，分别是2、1、2、3，发现没有规律，此时可以再结合考虑交点的个数，分别是1、3、3、3，发现也没有规律；这个时候考生不要轻易放弃，如果两组类型的点单独考虑起来都没有规律的话，那么我们再把它们相加或相减，看是否有规律；把它们相加，得到3、4、5、6，此时规律非常明显，接下来应是7个点，不分交点和切点，因此答案为A。
核心提示：交点和切点需要考生区分开来，切点的类型比较少，主要就是直线与曲线相切、曲线与曲线相切所形成的点；但交点的类型就比较多，主要包括直线与直线相交、直线与曲线相交和曲线与曲线相交所形成的点，而且每一种类型的交点中又分十字交叉点、丁字交叉点和角点三种形式，这些考生需要弄明白。
【例14】（2007年国考）
【一佳名师解析】此题答案为A。从整体上看，本题中有一个共同的规律，那就是有“出头”的情况，所谓“枪打出头鸟”，我们自然去数“出头端点”的个数，发现它们的个数分别是：
5 7 17
3 9 15
1 11 ？
此题的规律是按“S”型来看的，呈等差规律变化，于是“？”处应是13，因此答案为A。
【变14】（2008年国考）
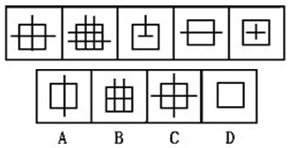
【一佳名师解析】此题答案为C。与上题类似，“出头端点”的个数分别是3、5、1、2、0、？，直接看没有什么规律，但把它们按从小到大的顺序排序的话就会有规律，即为0、1、2、3、？、5，于是“？”应为4，因此答案为C。
此题的数量规律是“乱序”，即要重排以后才呈现出等差或等比的规律。
核心提示：九宫格图形有两类路线：一类是“走直线”，包括横向、纵向和对角三个方向；另一类是“走曲线”，包括S型、G型和O型三种形式。其中，横向和纵向是最常见的推理路线。
【例1】（2010年国考）
【一佳名师解析】此题答案为A。从整体上看，本题中最明显的特征就是三角形这个元素，它们的数量分别是3、4、5、6、7、？，呈现出明显的规律，所以接下来应是8个三角形，因此答案为A。
【变1】（2011年4•24联考）
【一佳名师解析】此题答案为D。从整体上看，本题中最明显的特征就是含有圆和方两个基本元素，而且圆的个数明显都比方的个数要多，具体数一下是多2个，符合此规律的就是D项，因此答案为D。
核心提示：元素的个数一般可以重叠地数，只要数的元素不重复就可以了。
【例2】（2009年国考）
【一佳名师解析】此题答案为A。从第一、三、五个图来看，它们有两个共同的规律，那就是元素个数分别是2、3、4，元素种类数都是1；如果考虑元素的个数，那么第二、四个图都是有2个三角形，接下来应该也是2个相同元素，发现A、B、C都符合；于是考虑种类数，第二、四个图中都含有2种元素，接下来应该也是2种元素，发现只有A项符合，因此答案为A。
【变2】（2011年4•24联考）
【一佳名师解析】此题答案为A。如果考虑元素个数，此题同样无解，于是我们可以考虑种类数，发现每一个图都含有1类元素，因此答案为A。
需要注意的是，按属性的“曲直性”规律，我们可以得到一个不同于A项的答案，即B项，理由是前面所有的图都是“直线图”，而选项中只有B项是“直线图”，因此B项是一个答案。这就出现了“按不同的规律得出来的答案不同”这样的问题，对于这种问题，考生应按“最优规律”来选，一般来说，数量上的规律是很难“偶然”得到的，这才是出题者真正的意图所在。
核心提示：“相同或相似的图形为一类图”，这是判断种类数的一般规律。对于连在一起的图形，判断种类数时应拆分开来看，即按公共边剪开后再按前面的规律判断种类数。
【例3】（2008年浙江）
【一佳名师解析】此题答案为D。九宫格第一行的部分数都是1，第二行的部分数都是2，第三行前两个的部分数都是3，”？”处也应是3，因此答案为D。
【变3】（2011年4•24联考）
【一佳名师解析】此题答案为D。从整体上看，差不多每个图形组成都比较零散，很容易考虑到元素的个数（部分数），它们的个数分别是1、2、3、4、5、？，接下来应该是6，因此答案为D。
核心提示：在图形推理中，“连在一起的”就算一个部分。部分数可以归类为元素的个数。
【例4】（2009年国考）
【一佳名师解析】此题答案为C。从整体上看，有两类元素，而且在个数上存在变化，在第一组图中，圆的个数分别是4、2、0，五角星的个数分别是0、1、2，都是呈等差变化规律；同样，第二组图的圆的个数分别是4、2、？，五角星的个数分别是1、2、？，理应也呈等差变化规律，即有0个圆，3个五角星，因此答案为C。
实际上，此题存在着一种换算关系：一个五角星＝两个圆，于是，第一组都是4个圆，第二组都是6个圆，同样得出答案为C。
【变4】（2010年浙江）
【一佳名师解析】此题答案为A。如果考虑方向的话，此图中含有两类元素，一类是上三角，一类是下三角，而比较多的元素是下三角，所以我们希望能把前面的几个图都转变成下三角；由于第四个图有7个下三角，而第三个图只有2个上三角，所以不太可能是常数规律（因为都是7个下三角将不能按整数换算），考虑等差规律，而等差可能是递增的，也可能是递减的，需要试探：假设一个上三角＝三个下三角，那么换算结果是8、8、6、7，不成规律，因此考虑一个上三角＝四个下三角，那么换算结果是10、9、8、7，有规律，因此接下来应是6个下三角，因此答案为A。
核心提示：换算关系容易出现在图形中只含有两到三类元素的题目之中，而且元素的个数存在着一定的变化。换算关系一般不需要解方程，我们往往可以通过验证来得到答案，一般先按常数规律验证，否则按等差规律验证，一般把个数少的元素换成个数多的元素。
【例5】（2010年9•18联考）
【一佳名师解析】此题答案为C。从整体上看，图形中面的特征非常明显，于是考虑数封闭面的个数，发现它们都是4个，因此答案为C。
【变5】（2012年国考）
【一佳名师解析】此题答案为B。围绕汉字的考点很多，比如笔画数、部分数、封闭面数、结构关系和运算关系等，此题就是考查封闭面的个数，分别为2、3、4、5、？，接下来应该是6个封闭面，因此答案为B。
核心提示：封闭面一般是指“白面”，即那些被线段围成的空白面。
【例6】（2009年山东）
【一佳名师解析】此题答案为D。从整体上看，本题的图形中既有白面又有黑面，而且黑面的个数更少，分别是1、4、3、2、？，这是一个乱序数列，重新排列后“？”处应是5，即5个黑面，因此答案为D。
【变6】（2011年9•17联考）
【一佳名师解析】此题答案为B。在这种格状图中，有白格也有黑格，一般情况下我们优先考虑黑格，比如可以考虑黑格的个数，或黑格的移动等。此题中黑格个数变化比较大，优先去考虑它们的个数，即每一行的个数分别是2、4、4；4、4、6；6、2、？。初一看这些数字并没有什么规律，但整体上看，它们都是偶数，而奇偶性也是一个规律，选项中只有B项有偶数个黑格，因此答案为B。
核心提示：黑面个数的考查不多见，但考生还是要关注这个考点，看到黑白图形时可以从黑白两个方面进行思考。
【例7】（2009年4•26联考）
【一佳名师解析】此题答案为D。从整体上看，本题角的特征非常明显，于是考虑数角的个数，分别是9、9、9、9、？，显然，接下来也是9个角，因此答案为D。
【变7】（2010年江苏）
【一佳名师解析】此题答案为B。从整体上看，本题角的特征非常明显，优先考虑角的个数，前两行分别是1、4、3，4、5、6，发现只有一处不顺眼，即第一行第二个图，要是2的话，这个规律就自然了，再结合其他图角的特征，可以确定此题应是数“锐角”个数，于是”？”处应是9个锐角，毫无疑问答案是3个锐角三角形，因此答案为B。
核心提示：数角的时候需要注意，对于封闭图形来说，我们应该数“内角”，而对于非封闭图形来说，只要是一个角就要数。
【例8】（2010年4•25联考）
【一佳名师解析】此题答案为C。从整体上看，图形基本上都是多边形，考虑数边的个数，发现第一组图都是13条直线（段），第二组图的前两个图都是14条直线（段），于是“？”处也是14条直线（段），因此答案为C。
【变8】（2011年9•17联考）
【一佳名师解析】此题答案为C。本题中的图形都是由多边形构成的，而且每个图中均含有两个多边形，它们之间有叠交的部分，考生应该把重点放在这些特殊的叠交部分，发现叠交部分都是四边形，因此答案为C。
核心提示：线段包括直线段和曲线段两种，如果线段数比较多，我们应该尽量做乘法，如本题中的选项A有3×6－3＝15条直线段，B有3×5＝15条直线段。
【例9】（2008年浙江）
【一佳名师解析】此题答案为C。从整体上看，本题中所有的图都是曲线图，应数曲线段的个数，分别是1、2、3、4、？，接着应该是5，因此答案为C。
【变9】（2010年浙江）
【一佳名师解析】此题答案为B。与上一题相比，本题更具迷惑性，基本特征是有直线，也有曲线，还有不同的元素，直线基本上没有什么规律，考虑曲线段的个数，分别是3、3、3、3，很明显，我们要找一个含有3条曲线段的图形，因此答案为B。
核心提示：一段完整的圆弧（包括封闭的圆）就算一个曲线段。
【例10】（2009年4•26联考）
【一佳名师解析】此题答案为C。从整体上看，本题中所有的图形都是连在一起的，即为一个部分，因此答案为C。
实际上，上面九宫格中所有的图形都能够一笔画，“一笔画问题”是近年来国考和联考中喜欢考到的一个问题，考生要能够快速进行判断，即什么样的图形可以一笔画，不管这个图形多么复杂。关于一笔画的判定，早在1736年，著名的数学家欧拉就提出了解决办法，简单地说，就是“奇点数是0或2的图形可以一笔画”。
【变10】（2011年9•17联考）
【一佳名师解析】此题答案为C。与上一题相比，本题更具有隐蔽性，考生一般会从直线段的个数或面的个数这些常规的方向思考，但是都不能得到答案，此时我们可以考虑一笔画的问题，根据一笔画的判定标准，前面所有的图形都可以一笔画，比如第一个图形的奇点数为2（底上的两个顶点），后三个图形奇点数均为0，第五个图形奇点数为2（腰上的两个点），它们都能一笔画，而选项中A有4个奇点，B有6个奇点，C有0个奇点，D有4个奇点，因此答案为C。
核心提示：图形中的点有两种，一种是奇点，一种是偶点，按点的发散方向来确定，即如果一个点有奇数个发散方向，则这个点就是奇点，如果有偶数个发散方向，则为偶点。
【例11】（2012年国考）
【一佳名师解析】此题答案为D。本题考生可能会先考虑封闭面的个数，但没有规律，注意到第一行图都是一笔画图，第二行中都是两笔画图，第三行中前两个都是三笔画图，所以“？”处也是三笔画图，因此答案为D。
【变11】（2012年浙江）
【一佳名师解析】此题答案为B。与上题类似，本题的第一行也是一笔画图，第二行是两笔画图，第三行是三笔画图，因此答案为B。
核心提示：此题考到“多笔画”问题，实际上，在前面一笔画问题的基础上再进一步，我们不可以得到多笔画问题的判定，即“奇点数的个数是2N的图形可以N笔画”。
【例12】（2010年北京）
【一佳名师解析】此题答案为B。汉字或字母的笔画数与前面所说的一笔画和多笔画是不同的，这里需要单独分开来，汉字或字母的笔画数就按我们书写的习惯来确定，如本题的笔画数分别是13、11、9，呈等差变化，接着应是7，因此答案为B。
【变12】（2011年北京）
【一佳名师解析】此题答案为D。数一下汉字的笔画数，第一组分别是3、3、6，第二组分别是4、9、？，在第一组中，3＋3＝6，于是“？”处的笔画数为4＋9＝13，因此答案为D。
【例13】（2009年江苏）
【一佳名师解析】此题答案为B。本题考生的第一印象可能是去数封闭面的个数，它们确实有规律，分别是8、7、6、5、4、？，接着应该是3，但扫描选项发现没有3个面的图，所以此题并不是要求大家去数面；除面的特征明显外，此题“相交”的特征也很明显，于是考虑数交点的个数，分别是7、6、5、4、3、？，接着应该是2，B就有2个交点，因此答案为B。
【变13】（2009年浙江）
【一佳名师解析】此题答案为A。本题图形相切的特征比较明显，于是可以先考虑切点的个数，分别是2、1、2、3，发现没有规律，此时可以再结合考虑交点的个数，分别是1、3、3、3，发现也没有规律；这个时候考生不要轻易放弃，如果两组类型的点单独考虑起来都没有规律的话，那么我们再把它们相加或相减，看是否有规律；把它们相加，得到3、4、5、6，此时规律非常明显，接下来应是7个点，不分交点和切点，因此答案为A。
核心提示：交点和切点需要考生区分开来，切点的类型比较少，主要就是直线与曲线相切、曲线与曲线相切所形成的点；但交点的类型就比较多，主要包括直线与直线相交、直线与曲线相交和曲线与曲线相交所形成的点，而且每一种类型的交点中又分十字交叉点、丁字交叉点和角点三种形式，这些考生需要弄明白。
【例14】（2007年国考）
【一佳名师解析】此题答案为A。从整体上看，本题中有一个共同的规律，那就是有“出头”的情况，所谓“枪打出头鸟”，我们自然去数“出头端点”的个数，发现它们的个数分别是：
5 7 17
3 9 15
1 11 ？
此题的规律是按“S”型来看的，呈等差规律变化，于是“？”处应是13，因此答案为A。
【变14】（2008年国考）
【一佳名师解析】此题答案为C。与上题类似，“出头端点”的个数分别是3、5、1、2、0、？，直接看没有什么规律，但把它们按从小到大的顺序排序的话就会有规律，即为0、1、2、3、？、5，于是“？”应为4，因此答案为C。
此题的数量规律是“乱序”，即要重排以后才呈现出等差或等比的规律。
核心提示：九宫格图形有两类路线：一类是“走直线”，包括横向、纵向和对角三个方向；另一类是“走曲线”，包括S型、G型和O型三种形式。其中，横向和纵向是最常见的推理路线。
责编:一佳教育
- 上一篇：公务员考试行测图形推理——空间型
- 下一篇：公务员考试行测判断推理——造句法和代入法
