公务员考试行测数量关系——牛吃草问题
发布时间：2015-10-20 11:09:23 来源：一佳公务员考试网 点击量：
│
牛吃草问题是一个古老的数学问题，也是相对来说比较难的一类应用方程问题，它的原题是：“牧场上有一片青草，每天都生长得一样快。这片青草供给10头牛吃，可以吃22天，或者供给16头牛吃，可以吃10天，如果供给25头牛吃，可以吃几天？”
牛吃草问题的背后有一个基本的等式，即“消耗量＝新增量＋存量”，于是得到牛吃草问题的一个核心公式：M＝(c－a)×t，即存量＝（单位消耗量－单位新增量）×时间。为方便起见，一般假设每头牛（可以是其他动物或物体）在单位时间里（如每天、每周、每月、每年等，视具体情况而定）的消耗量为1，则草场上有多少头牛，其单位消耗量就是多少。
【例1】（2007年浙江）
林子里有猴子喜欢吃的野果，23只猴子可以在9周内吃光，21只猴子可以在12周内吃光，问如果有33只猴子一起吃，则需要几周吃光（假定野果生长的速度不变）？
A．2周 B．3周
C．4周 D．5周
【一佳名师解析】此题答案为C。设原来林子里的野果存量为M，野果的单位（周）新增量为a，则根据牛吃草公式，由前两个条件，有：M＝(23－a)×9，M＝(21－a)×12。
解得，a＝15，M＝72，再一次利用公式，有：72＝(33－15)×t，解得t＝4，因此答案为C。
【变1】（2009年广东）
某矿井发生透水事故，且矿井内每分钟涌出的水量相等。救援人员调来抽水机抽水，如果用2台抽水机抽水，预计40分钟可抽完；如果用4台同样的抽水机，16分钟可抽完。为赢得救援时间，要求在10分钟内抽完矿井内的水。那么至少需要抽水机（ ）。
A．5台 B．6台
C．8台 D．10台
【一佳名师解析】此题答案为B。设原来矿井里的水量为M，矿井内每分钟涌出的水量为a，则根据牛吃草公式，由前两个条件，有：
M＝(2－a)×40，M＝(4－a)×16。
解得，a＝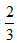
，M＝
，再一次利用公式，有：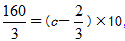
，解得c＝6，因此答案为B。
核心提示：三次利用牛吃草公式，一般都可以把这一类问题解决，其中前两个条件可以得出关键的两个量，第三个条件求要求的量。
【例2】（2009年国考）
一个水库在年降水量不变的情况下，能够维持全市12万人20年的用水量。在该市新迁入3万人之后，该水库只够维持15年的用水量。市政府号召节约用水，希望能将水库的使用寿命提高到30年。那么，该市市民平均需要节约多少比例的水才能实现政府制定的目标？
【一佳名师解析】此题答案为A。设水库的原有存量为M，年降水量为a，根据牛吃草公式，由前两个条件，有：
M＝(12－a)×20，M＝(15－a)×15。
解得，a＝3，M＝180，再次利用公式，并设节水比例为X，则有180＝[15(1－X)－3]×30，解得X＝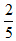
，因此答案为A。
【变2】（2008年江苏）
在春运高峰时，某客运中心售票大厅站满等待买票的旅客，为保证售票大厅的旅客安全，大厅入口处旅客排队以等速度进入大厅，按次序等待买票，买好票的旅客及时离开大厅。按照这种安排，如果开出10个售票窗口，5小时可使大厅内所有旅客买到票；如果开出12个售票窗口，3小时可使大厅内所有旅客买到票，假设每个窗口售票速度相同。如果大厅入口处旅客速度增加到原速度的1.5倍，在2小时内使大厅中所有旅客买到票，按这样的安排至少应开售票窗口数为（ ）。
A．15 B．16
C．18 D．19
【一佳名师解析】此题答案为C。设大厅里原有旅客存量为M，单位时间内旅客进入量为a，根据牛吃草公式，由前两个条件，有：
M＝(10－a)×5，M＝(12－a)×3。
解得，a＝7，M＝15，再次利用公式，此时a＝1.5×7＝10.5，设窗口数为c，则有15＝[c－10.5]×2，解得c＝18，因此答案为C。
核心提示：牛吃草问题在出题形式上有一个共同的特点，就是有两个已知条件，且已知条件一般是关于数量和时间的关系，问题会有不同的变化，考生要认清这种形式。
【例3】（2011年北京）
假设某地森林资源的增长速度是一定的，且不受到自然灾害等原因影响。那么若每年开采110万立方米，则可开采90年，若每年开采90万立方米则可开采210年。为了使这片森林可持续开发，则每年最多开采多少万立方米林木？
A．30 B．50
C．60 D．75
【一佳名师解析】此题答案为D。设这片森林原有存量为M，森林的年增长量为a，根据牛吃草公式，由前两个条件，有：
M＝(110－a)×90，M＝(90－a)×210。
解得，a＝75，M＝3150，由于问题是要求这片森林可持续开发，那么必须使每年的开采量不超过a，因此答案为D。
【变3】有一块草地，每天草生长的速度相同。现在这片牧草可供4头牛和8只羊吃8天，或者供7只牛和6只羊吃6天，或者12头牛和4只羊吃4天，那么这片草地可供10头牛和16只羊一起吃多少天？
A．4 B．3
C．2 D．1
【一佳名师解析】此题答案为B。设这块草地的原有存量为M，草的日生长量为a，牛、羊的日吃草量分别为1、c，根据牛吃草公式，由前三个条件，有：
M＝(4＋8c－a)×8，M＝(7＋6c－a)×6，M＝(12＋4c－a)×4。
解得，a＝2，c＝
，M＝48，再一次利用公式，有：48＝(10＋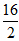
－2)×t，解得t＝3，因此答案为B。
核心提示：牛吃草问题会有很多创新之处，比如【例3】中的“可持续问题”和【变3】中的“多主体问题”。当“新增量＝消耗量”时，可以实现可持续发展；当设其中的一个主体单位时间消耗量为1时，可以转化为普通的牛吃草问题。
牛吃草问题的背后有一个基本的等式，即“消耗量＝新增量＋存量”，于是得到牛吃草问题的一个核心公式：M＝(c－a)×t，即存量＝（单位消耗量－单位新增量）×时间。为方便起见，一般假设每头牛（可以是其他动物或物体）在单位时间里（如每天、每周、每月、每年等，视具体情况而定）的消耗量为1，则草场上有多少头牛，其单位消耗量就是多少。
【例1】（2007年浙江）
林子里有猴子喜欢吃的野果，23只猴子可以在9周内吃光，21只猴子可以在12周内吃光，问如果有33只猴子一起吃，则需要几周吃光（假定野果生长的速度不变）？
A．2周 B．3周
C．4周 D．5周
【一佳名师解析】此题答案为C。设原来林子里的野果存量为M，野果的单位（周）新增量为a，则根据牛吃草公式，由前两个条件，有：M＝(23－a)×9，M＝(21－a)×12。
解得，a＝15，M＝72，再一次利用公式，有：72＝(33－15)×t，解得t＝4，因此答案为C。
【变1】（2009年广东）
某矿井发生透水事故，且矿井内每分钟涌出的水量相等。救援人员调来抽水机抽水，如果用2台抽水机抽水，预计40分钟可抽完；如果用4台同样的抽水机，16分钟可抽完。为赢得救援时间，要求在10分钟内抽完矿井内的水。那么至少需要抽水机（ ）。
A．5台 B．6台
C．8台 D．10台
【一佳名师解析】此题答案为B。设原来矿井里的水量为M，矿井内每分钟涌出的水量为a，则根据牛吃草公式，由前两个条件，有：
M＝(2－a)×40，M＝(4－a)×16。
解得，a＝
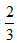，M＝，再一次利用公式，有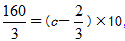：，解得c＝6，因此答案为B。核心提示：三次利用牛吃草公式，一般都可以把这一类问题解决，其中前两个条件可以得出关键的两个量，第三个条件求要求的量。
【例2】（2009年国考）
一个水库在年降水量不变的情况下，能够维持全市12万人20年的用水量。在该市新迁入3万人之后，该水库只够维持15年的用水量。市政府号召节约用水，希望能将水库的使用寿命提高到30年。那么，该市市民平均需要节约多少比例的水才能实现政府制定的目标？
【一佳名师解析】此题答案为A。设水库的原有存量为M，年降水量为a，根据牛吃草公式，由前两个条件，有：
M＝(12－a)×20，M＝(15－a)×15。
解得，a＝3，M＝180，再次利用公式，并设节水比例为X，则有180＝[15(1－X)－3]×30，解得X＝
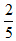，因此答案为A。【变2】（2008年江苏）
在春运高峰时，某客运中心售票大厅站满等待买票的旅客，为保证售票大厅的旅客安全，大厅入口处旅客排队以等速度进入大厅，按次序等待买票，买好票的旅客及时离开大厅。按照这种安排，如果开出10个售票窗口，5小时可使大厅内所有旅客买到票；如果开出12个售票窗口，3小时可使大厅内所有旅客买到票，假设每个窗口售票速度相同。如果大厅入口处旅客速度增加到原速度的1.5倍，在2小时内使大厅中所有旅客买到票，按这样的安排至少应开售票窗口数为（ ）。
A．15 B．16
C．18 D．19
【一佳名师解析】此题答案为C。设大厅里原有旅客存量为M，单位时间内旅客进入量为a，根据牛吃草公式，由前两个条件，有：
M＝(10－a)×5，M＝(12－a)×3。
解得，a＝7，M＝15，再次利用公式，此时a＝1.5×7＝10.5，设窗口数为c，则有15＝[c－10.5]×2，解得c＝18，因此答案为C。
核心提示：牛吃草问题在出题形式上有一个共同的特点，就是有两个已知条件，且已知条件一般是关于数量和时间的关系，问题会有不同的变化，考生要认清这种形式。
【例3】（2011年北京）
假设某地森林资源的增长速度是一定的，且不受到自然灾害等原因影响。那么若每年开采110万立方米，则可开采90年，若每年开采90万立方米则可开采210年。为了使这片森林可持续开发，则每年最多开采多少万立方米林木？
A．30 B．50
C．60 D．75
【一佳名师解析】此题答案为D。设这片森林原有存量为M，森林的年增长量为a，根据牛吃草公式，由前两个条件，有：
M＝(110－a)×90，M＝(90－a)×210。
解得，a＝75，M＝3150，由于问题是要求这片森林可持续开发，那么必须使每年的开采量不超过a，因此答案为D。
【变3】有一块草地，每天草生长的速度相同。现在这片牧草可供4头牛和8只羊吃8天，或者供7只牛和6只羊吃6天，或者12头牛和4只羊吃4天，那么这片草地可供10头牛和16只羊一起吃多少天？
A．4 B．3
C．2 D．1
【一佳名师解析】此题答案为B。设这块草地的原有存量为M，草的日生长量为a，牛、羊的日吃草量分别为1、c，根据牛吃草公式，由前三个条件，有：
M＝(4＋8c－a)×8，M＝(7＋6c－a)×6，M＝(12＋4c－a)×4。
解得，a＝2，c＝
，M＝48，再一次利用公式，有：48＝(10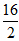＋－2)×t，解得t＝3，因此答案为B。核心提示：牛吃草问题会有很多创新之处，比如【例3】中的“可持续问题”和【变3】中的“多主体问题”。当“新增量＝消耗量”时，可以实现可持续发展；当设其中的一个主体单位时间消耗量为1时，可以转化为普通的牛吃草问题。
责编:一佳教育
- 上一篇：国家公务员考试行测判断推理之翻译型
- 下一篇：公务员考试行测数量关系每日一练
