公务员考试行测数量关系每日一练
发布时间：2015-10-24 13:44:18 来源：一佳公务员考试网 点击量：
│
平面几何问题
平面几何问题是几何问题中的重点，它主要考查多边形及圆的角度、距离、周长、面积等公式的计算及运用，因此考生有必要记住并理解一些基本的平面几何公式及定理。此外，“割补”思想在平面几何问题中也常有涉及，考生需要好好理解并掌握。
平面几何问题主要包括角边距问题、周长面积问题等两类问题，其中又以周长面积问题的考查最为常见。
角边距问题
角边距问题主要包括多边形的方位角问题、距离问题和多边形边长问题（特别是三角形）等。
【例1】（2011年9•17联考）
火车站点A和B与初始发车站C的直线距离都等于a km，站点A在发车站C的北偏东20度，站点B在发车站C的南偏东40度，若在站点A和站点B之间架设火车轨道，则最短的距离为（ ）。
【一佳名师解析】此题答案为D。根据题目中的方位及距离关系，以及“两点之间直线最短”，可以画出如下的图形：
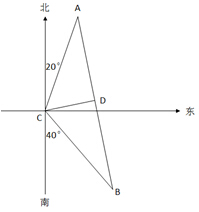容易求出∠ACB＝120度，作CD⊥AB于D，那么由∠A＝∠B＝30度，AC＝BC＝a，得到AD＝BD＝
，因此答案为D。
【变1】（2008年江苏）
台风中心从A地以每小时20公里的速度向东北方向移动，离台风中心30公里内的地区为危险区，城市B在A的正东40公里处，则B城处于危险区内的时间为多少小时？
A．1.5 B．1
C．0.5 D．2
【一佳名师解析】此题答案为B。根据题目中的方位及距离关系，可以画出如下的图：
其中AB＝40，BC＝BD＝30，BE⊥CD于E，当台风中心进入CD区域时，此时B城处理危险区域内，由于∠A＝45度，那么BE＝20
，进一步可以得到CE＝10（勾股定理），于是CD＝20，由于台风的速度是20公里/小时，所以它穿过CD区域的时间正好为1小时，因此答案为B。
核心提示：方位角要知道画，如“北偏东20度”，是从北向东画20度，而“东偏北30度”，是从东向北画30度。
【例2】（2011年4•24联考）
一条路上依次有A、B、C三个站点，加油站M恰好位于AC的中点，加油站N恰好位于BC的中点。若想知道M和N两个加油站之间的距离，只需要知道哪两点之间的距离？
A．C N B．B C
C．AM D．A B
【一佳名师解析】此题答案为D。对于此问题，我们首先要把问题中的图形画出来，如下图所示：
上图中，已知AM＝CM，BN＝CN，显然，MN＝CM－CN＝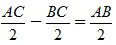
，故只要知道AB的距离就可以求得MN的距离，因此答案为D。
【变2】（2010年江西）
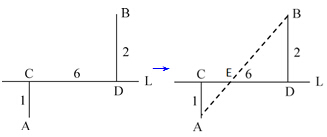
A、B两村庄分别在一条公路L的两侧，A到L的距离|AC|为1公里，B到L的距离|BD|为2公里，C、D两处相距6公里，欲在公路某处建一个垃圾站，使得A、B两个村庄到此处处理垃圾都比较方便，应建在离C处多少公里？
A．2.75 B．3.25
C．2 D．3
【一佳名师解析】此题答案为C。为了让A、B两个村庄到垃圾站处理垃圾都比较方便，必须使这两个村庄到垃圾站的总距离最短，显然，由“两点之间直线最短”，可知AB与CD的交点E就是理想的垃圾站选择处（右图所示）。由于△ACE和△BDE相似，于是有AC︰BD＝CE︰DE＝1︰2，结合条件CD＝6，易得CE＝2，因此答案为C。
核心提示：数形结合的思想很重要，很多题目，把图画出来，关系就一目了然，但凭空想像，却很难得到这些关系。
平面几何问题是几何问题中的重点，它主要考查多边形及圆的角度、距离、周长、面积等公式的计算及运用，因此考生有必要记住并理解一些基本的平面几何公式及定理。此外，“割补”思想在平面几何问题中也常有涉及，考生需要好好理解并掌握。
平面几何问题主要包括角边距问题、周长面积问题等两类问题，其中又以周长面积问题的考查最为常见。
角边距问题
角边距问题主要包括多边形的方位角问题、距离问题和多边形边长问题（特别是三角形）等。
【例1】（2011年9•17联考）
火车站点A和B与初始发车站C的直线距离都等于a km，站点A在发车站C的北偏东20度，站点B在发车站C的南偏东40度，若在站点A和站点B之间架设火车轨道，则最短的距离为（ ）。
【一佳名师解析】此题答案为D。根据题目中的方位及距离关系，以及“两点之间直线最短”，可以画出如下的图形：
，因此答案为D。【变1】（2008年江苏）
台风中心从A地以每小时20公里的速度向东北方向移动，离台风中心30公里内的地区为危险区，城市B在A的正东40公里处，则B城处于危险区内的时间为多少小时？
A．1.5 B．1
C．0.5 D．2
【一佳名师解析】此题答案为B。根据题目中的方位及距离关系，可以画出如下的图：
，进一步可以得到CE＝10（勾股定理），于是CD＝20，由于台风的速度是20公里/小时，所以它穿过CD区域的时间正好为1小时，因此答案为B。核心提示：方位角要知道画，如“北偏东20度”，是从北向东画20度，而“东偏北30度”，是从东向北画30度。
【例2】（2011年4•24联考）
一条路上依次有A、B、C三个站点，加油站M恰好位于AC的中点，加油站N恰好位于BC的中点。若想知道M和N两个加油站之间的距离，只需要知道哪两点之间的距离？
A．C N B．B C
C．AM D．A B
【一佳名师解析】此题答案为D。对于此问题，我们首先要把问题中的图形画出来，如下图所示：
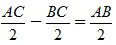，故只要知道AB的距离就可以求得MN的距离，因此答案为D。【变2】（2010年江西）
A、B两村庄分别在一条公路L的两侧，A到L的距离|AC|为1公里，B到L的距离|BD|为2公里，C、D两处相距6公里，欲在公路某处建一个垃圾站，使得A、B两个村庄到此处处理垃圾都比较方便，应建在离C处多少公里？
A．2.75 B．3.25
C．2 D．3
【一佳名师解析】此题答案为C。为了让A、B两个村庄到垃圾站处理垃圾都比较方便，必须使这两个村庄到垃圾站的总距离最短，显然，由“两点之间直线最短”，可知AB与CD的交点E就是理想的垃圾站选择处（右图所示）。由于△ACE和△BDE相似，于是有AC︰BD＝CE︰DE＝1︰2，结合条件CD＝6，易得CE＝2，因此答案为C。
核心提示：数形结合的思想很重要，很多题目，把图画出来，关系就一目了然，但凭空想像，却很难得到这些关系。
责编:一佳教育
- 上一篇：公务员考试行测数量关系——牛吃草问题
- 下一篇：公务员考试行测判断推理——匹配型
