公务员考试行测数量关系——周长面积问题
发布时间：2015-10-30 11:18:59 来源：一佳公务员考试网 点击量：
│
周长和面积往往是放在一起来考查的，所以我们这里把它们作为一个问题来对待，考生需要熟悉一些常见图形的周长面积计算公式，特别是正多边形（如三角形）和圆。
【例1】（2009年北京）
从一块正方形木板上锯下宽5cm的一个木条后，剩下的长方形面积是750cm2，锯下的木条面积是多少平方厘米？
A．25 B．150
C．152 D．168
【一佳名师解析】此题答案为B，因子法可解。由于正方形的面积等于边长的平方，即是一个平方数，那么剩下的长方形面积加上锯下的长方形面积一定要是一个平方数，只有B项符合（750＋150＝900＝302），代入验证一下（5×30＝150，25×30＝750），B项确实符合题目要求，因此答案为B。
【变1】（2009年浙江）
下图是由5个相同的小长方形拼成的大长方形，大长方形的周长是88厘米，问大长方形的面积是多少平方厘米？
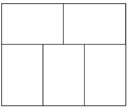
A．472平方厘米 B．476平方厘米
C．480平方厘米 D．484平方厘米
【一佳名师解析】此题答案为C，因子法可解。由于5个小长方形是一样的，那么大长方形的面积应是5的倍数，根据优整思想，只有C项是5的倍数，代入验证一下（每个小长方形的面积为
＝96，当长是12，宽是8就符合要求），C项确实符合题目要求，因此答案为C。
核心提示：“优整”思想在几何问题中也很重要，当题目和选项中的数据都是整数，那么答案也是整数的可能性也非常大，只是要警惕含根号的情况，可能需要代入验证。
【例2】（2010上半年联考）
一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的（ ）。
【一佳名师解析】此题答案为B。由于正三角形和正六边形的具体周长未知，故可以考虑特殊化，即假设正六边形的边长为1，则正三角形的边长为2。显然，我们可以直接利用公式法来计算得到正三角形和正六边形的面积，但这不是最明智的方法，因为计算容易出错，且浪费时间，注意到正六边形可以由6个边长为1的小正三角形得到，而正三角形也能由4个边长为1的小正三角形得到，如下图所示：
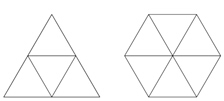
显然，正六边形和正三角形的面积之比＝6︰4＝3︰2，即1.5倍的关系，因此答案为B。
【变2】（2007年浙江）
如图所示，长方形ACEG被线段BF、HD分成四个大小不等的小长方形。已知AH为6cm，GF为3cm，DE为10cm，BC为7cm。则三角形ICG的面积为（ ）。
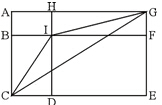
A．32cm2 B．28cm2
C．30cm2 D．26cm2
【一佳名师解析】此题答案为D。显然△ICG是一个不规则三角形，直接求解不太明智，直接分割也不方便，注意到△ICG在一个更大的△CAG里面，且△CBI和四边形BAGI是规则图形，于是有：S△ICG＝S△CAG－S△CBI－S梯形BAGI＝80－21－33＝26，因此答案为D。
核心提示：几何图形的“分割”很重要，对于规则的图形，我们往往把它分割成标准的基本单元（一般是三角形，因为三角形是最简单的多边形）。
【例3】（2007年广西）
三个圆的半径都是5cm，三个圆两两相交于圆心，求阴影部分的面积之和（ ）。
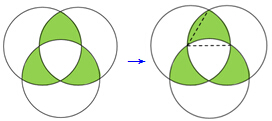
A．29.25cm2 B．33.25cm2
C．39.25cm2 D．35.35cm2
【一佳名师解析】此题答案为C。因为问题中的图形是不规则图形，且含有曲线部分，故考虑通过割补法，把它转化为一个规则图形进行计算。由于三个阴影部分是一样的，故我们只要求出其中的一个阴影面积即可，通过连接交点，可以得到解题思路，如右图所示。显然，两条虚线的长度是一样的（等于圆的半径），那么它们所围成的弧面面积必然相同，把多出来的弧面切下来“补”到空白的弧面处，就可以得到一个扇形，且扇形的圆心角为60度，那么三个这样的扇形正好构成一个半圆，它们的面积是π×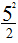
≈39.25 cm2，因此答案为C。
【变3】（2009年4•26联考）
如图所示，大圆的半径是8，求阴影部分的面积是多少？
A．120 B．128
C．136 D．144
【一佳名师解析】此题答案为B。和上题类似，我们可以求出其中的一个阴影部分的面积，如右图所示。通过割补，每一个小图都等价于一个正方形，且正方形的对角线就是圆的直径，于是由菱形的面积计算公式，每个小正方形的面积为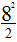
＝32，于是4个这样的图形加起来就是32×4＝128，因此答案为B。
核心提示：“割补”思想是一种等价转换的思想，即把多的地方割下来，补到少的地方去，得到一个规则的图形进行等价求解。对于弧面图形，往往是通过连接弧线交点来得到解题思路。
【例1】（2009年北京）
从一块正方形木板上锯下宽5cm的一个木条后，剩下的长方形面积是750cm2，锯下的木条面积是多少平方厘米？
A．25 B．150
C．152 D．168
【一佳名师解析】此题答案为B，因子法可解。由于正方形的面积等于边长的平方，即是一个平方数，那么剩下的长方形面积加上锯下的长方形面积一定要是一个平方数，只有B项符合（750＋150＝900＝302），代入验证一下（5×30＝150，25×30＝750），B项确实符合题目要求，因此答案为B。
【变1】（2009年浙江）
下图是由5个相同的小长方形拼成的大长方形，大长方形的周长是88厘米，问大长方形的面积是多少平方厘米？
A．472平方厘米 B．476平方厘米
C．480平方厘米 D．484平方厘米
【一佳名师解析】此题答案为C，因子法可解。由于5个小长方形是一样的，那么大长方形的面积应是5的倍数，根据优整思想，只有C项是5的倍数，代入验证一下（每个小长方形的面积为
＝96，当长是12，宽是8就符合要求），C项确实符合题目要求，因此答案为C。核心提示：“优整”思想在几何问题中也很重要，当题目和选项中的数据都是整数，那么答案也是整数的可能性也非常大，只是要警惕含根号的情况，可能需要代入验证。
【例2】（2010上半年联考）
一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的（ ）。
【一佳名师解析】此题答案为B。由于正三角形和正六边形的具体周长未知，故可以考虑特殊化，即假设正六边形的边长为1，则正三角形的边长为2。显然，我们可以直接利用公式法来计算得到正三角形和正六边形的面积，但这不是最明智的方法，因为计算容易出错，且浪费时间，注意到正六边形可以由6个边长为1的小正三角形得到，而正三角形也能由4个边长为1的小正三角形得到，如下图所示：
显然，正六边形和正三角形的面积之比＝6︰4＝3︰2，即1.5倍的关系，因此答案为B。
【变2】（2007年浙江）
如图所示，长方形ACEG被线段BF、HD分成四个大小不等的小长方形。已知AH为6cm，GF为3cm，DE为10cm，BC为7cm。则三角形ICG的面积为（ ）。
A．32cm2 B．28cm2
C．30cm2 D．26cm2
【一佳名师解析】此题答案为D。显然△ICG是一个不规则三角形，直接求解不太明智，直接分割也不方便，注意到△ICG在一个更大的△CAG里面，且△CBI和四边形BAGI是规则图形，于是有：S△ICG＝S△CAG－S△CBI－S梯形BAGI＝80－21－33＝26，因此答案为D。
核心提示：几何图形的“分割”很重要，对于规则的图形，我们往往把它分割成标准的基本单元（一般是三角形，因为三角形是最简单的多边形）。
【例3】（2007年广西）
三个圆的半径都是5cm，三个圆两两相交于圆心，求阴影部分的面积之和（ ）。
A．29.25cm2 B．33.25cm2
C．39.25cm2 D．35.35cm2
【一佳名师解析】此题答案为C。因为问题中的图形是不规则图形，且含有曲线部分，故考虑通过割补法，把它转化为一个规则图形进行计算。由于三个阴影部分是一样的，故我们只要求出其中的一个阴影面积即可，通过连接交点，可以得到解题思路，如右图所示。显然，两条虚线的长度是一样的（等于圆的半径），那么它们所围成的弧面面积必然相同，把多出来的弧面切下来“补”到空白的弧面处，就可以得到一个扇形，且扇形的圆心角为60度，那么三个这样的扇形正好构成一个半圆，它们的面积是π×
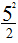≈39.25 cm2，因此答案为C。【变3】（2009年4•26联考）
如图所示，大圆的半径是8，求阴影部分的面积是多少？
A．120 B．128
C．136 D．144
【一佳名师解析】此题答案为B。和上题类似，我们可以求出其中的一个阴影部分的面积，如右图所示。通过割补，每一个小图都等价于一个正方形，且正方形的对角线就是圆的直径，于是由菱形的面积计算公式，每个小正方形的面积为
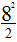＝32，于是4个这样的图形加起来就是32×4＝128，因此答案为B。核心提示：“割补”思想是一种等价转换的思想，即把多的地方割下来，补到少的地方去，得到一个规则的图形进行等价求解。对于弧面图形，往往是通过连接弧线交点来得到解题思路。
责编:一佳教育
- 上一篇：公务员考试行测判断推理——匹配型
- 下一篇：公务员考试行测判断推理之运算型
