公务员考试行测数量关系——表面切面问题
发布时间：2015-11-15 14:47:41 来源：一佳公务员考试网 点击量：
│
表面问题是指立体图形外表面的求解问题，而切面问题是指立体图形的内切面的求解问题，它们均属于面积问题的空间化。
【例1】（2010年4•25联考）
将边长为1的正方体一刀切割为2个多面体，其表面积之和最大为（ ）。
【一佳名师解析】此题答案为A。切割成2个多面体后，表面积之和会等于原来正方体的外表面加上2倍的切面，由于原来正方体的外表面为6，那么现在关键是求出最大的切面面积。切面有多种切法，如下图所示：
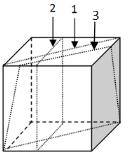有两类切法，第一类是平行切（相对于棱边），第二类是非平行切，其中第1种和第2种是平行切，显然第1种的切面大于第2种（高度一样，但对角线最长），至于第3种切法和第2种切法的比较则相对比较困难，因为它们的边长及高都不相同，但是注意到第3种切法中，边长的缩短速度要大于高的增长速度（边长是线性缩短，高是根号缩短），因此无论怎么变化，第3种切面均小于第1种，故最大的切面面积为第1种，即
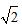，因此答案为A。
【变1】（2011年国考）
用一个平面将一个边长为1的正四面体切分为两个完全相同的部分，则切面的最大面积为（ ）。
【一佳名师解析】此题答案为B，估算法可解。由题目提供的信息，可以画出如下的图形：
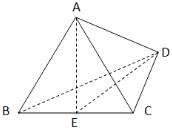显然，我们可以按部就班地把切面面积算出来，但过程相对繁琐，注意到切面面积肯定会小于任一个侧面面积（极端化考虑，即把E点移动到B点或C点，很明显在AD长度不变的情况下，只有AED的高是最短的，于是其面积自然会小于侧面面积），容易求得边长是1的正三角形（即侧面）的面积是
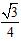，于是我们需要选一个稍微小于它的答案，因此答案为B。
核心提示：多面体的最大切面往往是沿其中一个面的对角线方向切入。
【例2】（2007年国考）
现有边长1米的一个木质正方体，已知将其放入水里，将有0.6米浸入水中。如果将其分割成边长0.25米的小正方体，并将所有的小正方体都放入水中，直接和水接触的表面积总量为（ ）。
A．3.4平方米 B．9.6平方米
C．13.6平方米 D．16平方米
【一佳名师解析】此题答案为C，因子法可解。由物理学中的浮力定理，只要物体密度相同，那么相似的物体浸入水中的体积会成一定比例。由于分割的小正方体与原来的大正方体完全相似，故直接与水接触的表面积也会和原来大正方体直接和水接触的表面积成一定比例，而原来的大正方体直接和水接触的表面积为0.6×1×4＋1×1＝3.4平方米，那么由倍数法则，所有小正方体的直接和水接触的表面积必定含有3.4的因子，排除选项B和D；显然，所有小正方体的直接和水接触的表面积肯定会大于原来的表面积3.4，因此答案为C。
【变2】（2007年广东）
一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的2倍，那么这个长方体的表面积是（ ）。
A．74 B．148
C．150 D．154
【一佳名师解析】此题答案为B，方程法可解。设长方体的长、宽、高分别为X＋1、X、X－1，于是长、宽、高之和为3X，所有棱长之和为4×3X＝12X，体积为X(X2－1)，根据题意，有X(X2－1)＝2×12X，解得X＝5，那么长、宽、高分别是6、5、4，由于长方体有3对面，于是它的表面积之和为2×(6×5＋6×4＋5×4)＝148，因此答案为B。
核心提示：六面体是最常考的多面体，考生需要熟悉它的面和棱的关系，即六面体有3对面，有4对棱。
【例1】（2010年4•25联考）
将边长为1的正方体一刀切割为2个多面体，其表面积之和最大为（ ）。
【一佳名师解析】此题答案为A。切割成2个多面体后，表面积之和会等于原来正方体的外表面加上2倍的切面，由于原来正方体的外表面为6，那么现在关键是求出最大的切面面积。切面有多种切法，如下图所示：
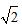，因此答案为A。【变1】（2011年国考）
用一个平面将一个边长为1的正四面体切分为两个完全相同的部分，则切面的最大面积为（ ）。
【一佳名师解析】此题答案为B，估算法可解。由题目提供的信息，可以画出如下的图形：
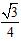，于是我们需要选一个稍微小于它的答案，因此答案为B。核心提示：多面体的最大切面往往是沿其中一个面的对角线方向切入。
【例2】（2007年国考）
现有边长1米的一个木质正方体，已知将其放入水里，将有0.6米浸入水中。如果将其分割成边长0.25米的小正方体，并将所有的小正方体都放入水中，直接和水接触的表面积总量为（ ）。
A．3.4平方米 B．9.6平方米
C．13.6平方米 D．16平方米
【一佳名师解析】此题答案为C，因子法可解。由物理学中的浮力定理，只要物体密度相同，那么相似的物体浸入水中的体积会成一定比例。由于分割的小正方体与原来的大正方体完全相似，故直接与水接触的表面积也会和原来大正方体直接和水接触的表面积成一定比例，而原来的大正方体直接和水接触的表面积为0.6×1×4＋1×1＝3.4平方米，那么由倍数法则，所有小正方体的直接和水接触的表面积必定含有3.4的因子，排除选项B和D；显然，所有小正方体的直接和水接触的表面积肯定会大于原来的表面积3.4，因此答案为C。
【变2】（2007年广东）
一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的2倍，那么这个长方体的表面积是（ ）。
A．74 B．148
C．150 D．154
【一佳名师解析】此题答案为B，方程法可解。设长方体的长、宽、高分别为X＋1、X、X－1，于是长、宽、高之和为3X，所有棱长之和为4×3X＝12X，体积为X(X2－1)，根据题意，有X(X2－1)＝2×12X，解得X＝5，那么长、宽、高分别是6、5、4，由于长方体有3对面，于是它的表面积之和为2×(6×5＋6×4＋5×4)＝148，因此答案为B。
核心提示：六面体是最常考的多面体，考生需要熟悉它的面和棱的关系，即六面体有3对面，有4对棱。
责编:一佳教育
