2016年江西省招警考试行测数量关系：容斥问题
发布时间：2015-12-21 11:09:37 来源：一佳公务员考试网 点击量：
│
容斥问题是关于集合与集合之间运算关系的一类问题，从出题形式上看，它又分为两集合的容斥问题、三集合的容斥问题和多集合的容斥问题，其中前两类问题是相似的，需要考生掌握两集合与三集合的容斥原理，第三类问题有所不同，需要考生从反面来考虑问题。下面是考生必须掌握的容斥原理，我们用“文氏图”来理解：
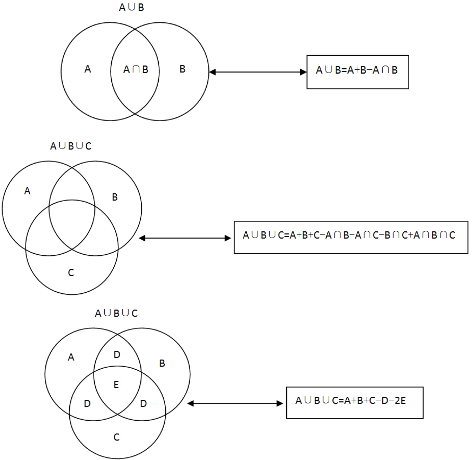两集合的关系很容易理解，关键是三集合的容斥原理，上面给出了两个关系。其中第二个图是标准的三集合容斥原理，别看式子很长，记住它即很容易，即“加奇减偶”的关系：奇数个集合的交（包括单个集合）前面是用加法，偶数个集合的交前面是用减法。其实，更多集合的标准容斥原理都是“加奇减偶”的关系；第三个图是没有重叠关系的容斥原理，所以式子更简单，D区域表示同时满足两个关系的集合，而E区域表示同时满足三个关系的集合，如A、B、C表示语文、数学、英语考试及格的人数，则D表示正好有两门考试及格的人数，E区域表示三门考试都及格的人数，显然，在A＋B＋C的过程中，D多加了一次，E多加了两次，那么多加了就应该减去，多加了几次就应该减去几次，前面的关系都可以这样来理解。
【例1】（2006年国考）
现有50名学生都做物理、化学实验，如果物理实验做正确的有40人，化学实验做正确的有31人，两种实验都做错的有4人，则两种实验都做对的有（ ）。
A．27人 B．25人
C．19人 D．10人
【一佳名师解析】此题答案为B。显然，总人数＝至少有一种实验做对的人数＋两种实验都做错的人数，设两种实验都做对的人数为X人，则由两集合容斥原理，至少有一种实验做对的人数为40＋31－X人，于是有40＋31－X＋4＝50，解得X＝25人，因此答案为B。
【变1】（2008年海南）
某班共有50名学生参加数学和外语两科考试，已知数学成绩及格的有40人，外语成绩及格的有25人，据此可知数学成绩及格而外语成绩不及格者（ ）。
A．至少有10人 B．至少有15人
C．有20人 D．至多有30人
【一佳名师解析】此题答案为B。这道题的考法比较灵活，考虑数学和外语及格人数的关系，结合文氏图，此题很容易解决，如下图所示：
上图中列出了三个移动的状态1、2、3，显然，在状态3的时候数学及格而外语不及格的人数达到最少，为40－25＝15人，因此答案为B。
核心提示：建议考生通过文氏图来理解容斥原理，这样的话，即使在考试时忘记了容斥原理，考生也可以通过文氏图把题目做出来。
【例2】（2009年国考）
如下图所示，X、Y、Z分别是面积为64、180、160的三张不同形状的纸片。它们部分重叠放在一起盖在桌面上，总共盖住的面积为290。且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36。问阴影部分的面积是多少？
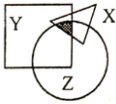A．15 B．16 C．14 D．18
【一佳名师解析】此题答案为B。本题的关系非常清楚，故考虑直接利用公式法。由于X∪Y∪Z＝X＋Y＋Z－X∩Y－X∩Z－Y∩Z＋X∩Y∩Z，于是X∩Y∩Z＝290－64－180－160＋24＋70＋36，尾数是6，因此答案为B。
【变2】（2012年4•21联考）
某公司招聘员工，按规定每人至多可投考两个职位，结果共42人报名，甲、乙、丙三个职位报名人数分别是22人、16人、25人，其中同时报甲、乙职位的人数为8人，同时报甲、丙职位的人数为6人，那么同时报乙、丙职位的人数为（ ）。
A．7人 B．8人
C．5人 D．6人
【一佳名师解析】此题答案为A。这是一道带附加条件的容斥问题，其附加条件是“每人至多可投考两个职位”，于是没有人报三个职位，即“甲∩乙∩丙＝0”，设同时报乙、丙职位的人数为X人，那么直接利用三集合容斥原理，有：42＝22＋16＋25－8－6－X，尾数是7，因此答案为A。
核心提示：熟悉公式是快速解决这一类问题的关键，但前提是考生需要充分理解文氏图中每一个区域的具体含义，在最后计算时结合使用尾数法。
【例3】（2011年国考）
某市对52种建筑防水卷材产品进行质量抽检，其中有8种产品的低温柔度不合格，10种产品的可溶物含量不达标，9种产品的接缝剪切性能不合格，同时两项不合格的有7种，有1种产品这三项都不合格。则三项全部合格的建筑防水卷材产品有多少种？
A．37 B．36
C．35 D．34
【一佳名师解析】此题答案为D。本题的关系如下图所示：
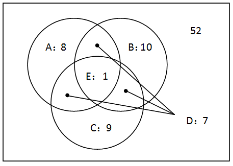问题是求合格产品的数量，那么首先要求出至少有一种产品不合格的数量A∪B∪C，由三集合容斥原理，有A∪B∪C＝A＋B＋C－D－2E＝8＋10＋9－7－2＝18，所以合格产品的数量为52－18＝34种，因此答案为D。
【变3】（2010年国考）
某高校对一些学生进行问卷调查。在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备选择两种考试参加的有46人，不参加其中任何一种考试的有15人。问接受调查的学生共有多少人？
A．120 B．144
C．177 D．192
【一佳名师解析】此题答案为A。和上题类似，接受调查的总人数＝至少参加一种考试的人数＋不参加其中任何一种考试的人数，那么由三集合容斥原理，可以求得至少参加一种考试的人数为63＋89＋47－46－2×24，尾数是5，再加上不参加的15人，尾数是0，因此答案为A。
【例4】（2010下半年联考）
某社团共有46人，其中35人爱好戏剧，30人爱好体育，38人爱好写作，40人爱好收藏，这个社团至少有多少人以上四项活动都喜欢？
A．5 B．6
C．7 D．8
【一佳名师解析】此题答案为A。这是一个四集合的容斥关系，很明显，直接从正面考虑会遇到困难，因为题目提供的条件不够，考虑从反面着手。易知不爱好戏剧、体育、写作和收藏的人分别为11人、16人、8人和6人，显然，至少有一项活动不都喜欢的人数最多有11＋16＋8＋6＝41人（现实情况下可能有重复，达不到41个人），此时只有5个人四项活动都喜欢，因此答案为A。
【变4】（2008年国考）
共有100个人参加某公司的招聘考试，考试内容共有5道题，1－5题分别有80人，92人，86人，78人，和74人答对，答对了3道和3道以上的人员能通过考试，请问至少有多少人能通过考试？
A．30 B．55
C．70 D．74
【一佳名师解析】此题答案为C。和上题类似，我们需要从反面考虑，即考虑不通过考试的人数最多有多少人。因为答错3道或3道以上的人不能通过考试，而答错的题目总共有20＋8＋14＋22＋26＝90题，所以不通过考试的人数最多有90/3=30人（即考虑刚好不通过的情况，就是每个人正好答错3道题），那么通过考试的人数最少是70人，因此答案为C。
核心提示：多集合容斥问题一般会结合极端法来做，而解决这类问题的关键是从问题的反面着手，这里也体现了“互补”的思想。
【例1】（2006年国考）
现有50名学生都做物理、化学实验，如果物理实验做正确的有40人，化学实验做正确的有31人，两种实验都做错的有4人，则两种实验都做对的有（ ）。
A．27人 B．25人
C．19人 D．10人
【一佳名师解析】此题答案为B。显然，总人数＝至少有一种实验做对的人数＋两种实验都做错的人数，设两种实验都做对的人数为X人，则由两集合容斥原理，至少有一种实验做对的人数为40＋31－X人，于是有40＋31－X＋4＝50，解得X＝25人，因此答案为B。
【变1】（2008年海南）
某班共有50名学生参加数学和外语两科考试，已知数学成绩及格的有40人，外语成绩及格的有25人，据此可知数学成绩及格而外语成绩不及格者（ ）。
A．至少有10人 B．至少有15人
C．有20人 D．至多有30人
【一佳名师解析】此题答案为B。这道题的考法比较灵活，考虑数学和外语及格人数的关系，结合文氏图，此题很容易解决，如下图所示：
核心提示：建议考生通过文氏图来理解容斥原理，这样的话，即使在考试时忘记了容斥原理，考生也可以通过文氏图把题目做出来。
【例2】（2009年国考）
如下图所示，X、Y、Z分别是面积为64、180、160的三张不同形状的纸片。它们部分重叠放在一起盖在桌面上，总共盖住的面积为290。且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36。问阴影部分的面积是多少？
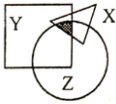
【一佳名师解析】此题答案为B。本题的关系非常清楚，故考虑直接利用公式法。由于X∪Y∪Z＝X＋Y＋Z－X∩Y－X∩Z－Y∩Z＋X∩Y∩Z，于是X∩Y∩Z＝290－64－180－160＋24＋70＋36，尾数是6，因此答案为B。
【变2】（2012年4•21联考）
某公司招聘员工，按规定每人至多可投考两个职位，结果共42人报名，甲、乙、丙三个职位报名人数分别是22人、16人、25人，其中同时报甲、乙职位的人数为8人，同时报甲、丙职位的人数为6人，那么同时报乙、丙职位的人数为（ ）。
A．7人 B．8人
C．5人 D．6人
【一佳名师解析】此题答案为A。这是一道带附加条件的容斥问题，其附加条件是“每人至多可投考两个职位”，于是没有人报三个职位，即“甲∩乙∩丙＝0”，设同时报乙、丙职位的人数为X人，那么直接利用三集合容斥原理，有：42＝22＋16＋25－8－6－X，尾数是7，因此答案为A。
核心提示：熟悉公式是快速解决这一类问题的关键，但前提是考生需要充分理解文氏图中每一个区域的具体含义，在最后计算时结合使用尾数法。
【例3】（2011年国考）
某市对52种建筑防水卷材产品进行质量抽检，其中有8种产品的低温柔度不合格，10种产品的可溶物含量不达标，9种产品的接缝剪切性能不合格，同时两项不合格的有7种，有1种产品这三项都不合格。则三项全部合格的建筑防水卷材产品有多少种？
A．37 B．36
C．35 D．34
【一佳名师解析】此题答案为D。本题的关系如下图所示：
【变3】（2010年国考）
某高校对一些学生进行问卷调查。在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备选择两种考试参加的有46人，不参加其中任何一种考试的有15人。问接受调查的学生共有多少人？
A．120 B．144
C．177 D．192
【一佳名师解析】此题答案为A。和上题类似，接受调查的总人数＝至少参加一种考试的人数＋不参加其中任何一种考试的人数，那么由三集合容斥原理，可以求得至少参加一种考试的人数为63＋89＋47－46－2×24，尾数是5，再加上不参加的15人，尾数是0，因此答案为A。
【例4】（2010下半年联考）
某社团共有46人，其中35人爱好戏剧，30人爱好体育，38人爱好写作，40人爱好收藏，这个社团至少有多少人以上四项活动都喜欢？
A．5 B．6
C．7 D．8
【一佳名师解析】此题答案为A。这是一个四集合的容斥关系，很明显，直接从正面考虑会遇到困难，因为题目提供的条件不够，考虑从反面着手。易知不爱好戏剧、体育、写作和收藏的人分别为11人、16人、8人和6人，显然，至少有一项活动不都喜欢的人数最多有11＋16＋8＋6＝41人（现实情况下可能有重复，达不到41个人），此时只有5个人四项活动都喜欢，因此答案为A。
【变4】（2008年国考）
共有100个人参加某公司的招聘考试，考试内容共有5道题，1－5题分别有80人，92人，86人，78人，和74人答对，答对了3道和3道以上的人员能通过考试，请问至少有多少人能通过考试？
A．30 B．55
C．70 D．74
【一佳名师解析】此题答案为C。和上题类似，我们需要从反面考虑，即考虑不通过考试的人数最多有多少人。因为答错3道或3道以上的人不能通过考试，而答错的题目总共有20＋8＋14＋22＋26＝90题，所以不通过考试的人数最多有90/3=30人（即考虑刚好不通过的情况，就是每个人正好答错3道题），那么通过考试的人数最少是70人，因此答案为C。
核心提示：多集合容斥问题一般会结合极端法来做，而解决这类问题的关键是从问题的反面着手，这里也体现了“互补”的思想。
责编:一佳教育
