2016年江西省招警考试数量关系：排列组合问题
发布时间：2015-12-31 10:48:53 来源：一佳公务员考试网 点击量：
│
排列组合问题是一类很广泛很实用的问题，但这类问题往往会比较难，主要原因是考生对其中的一些计数现象缺乏深入思考。掌握排列组合问题，需要考生理解和掌握排列组合问题中的“两原理、两计算、两思想和三方法”，现简要介绍之。
1．两原理：加法原理和乘法原理
加法原理是一种分类的思想，基本关系是：总个数＝每一类的个数之和。
乘法原理是一种分步的思想，基本关系是：总个数＝每一步的个数之积。
举例：从A地去B地，可选的交通工具有火车、汽车、飞机、轮船，且它们的班次数分别有4、5、2、1个，那么从A地去B地总共的方法数为4＋5＋2＋1＝12种（加法原理——分类）；如果从A地去B地必须中转C地，且从A地去C地有3种交通工具可选，从C地去B地有4种交通工具可选，那么从A地去B地总共的方法数为3×4＝12种（乘法原理——分步）。
2．两计算：排列数和组合数计算
排列讲究先后顺序，用乘法原理可以理解它，其计算式为：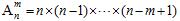
。
上面是非封闭区间的排列公式，如果是封闭区间（如圆圈），那么还要再除以m（想想为什么？）。
组合不讲究先后顺序，其计算式为：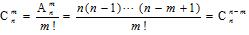
。
举例：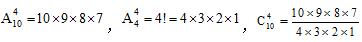
3．两思想：分类讨论思想和互补思想
分类讨论思想是排列组合问题中的基本思想，很多问题都需要分类讨论，分类要找准角度，思维要严谨，做到不重不漏。
互补思想是一种重要的思想，它适用的一般情况是“整体＝一部分＋另一部分”，而问题是求“一部分”，那么我们通过求解“整体”和“另一部分”来间接求出问题。这种思想在前面的几何问题和容斥问题当中已有体现。
4．三方法：捆绑法、隔板法和插空法
这三种方法是排列组合问题中的经典方法，我们在高中数学的时候学习过，现重温一下。
(1) 捆绑法
捆绑法是指一些有特殊要求的元素需要安排在一起，那么我们先将这些元素“捆绑”在一起视为一个元素，参与其他元素的排列（外部排列），因捆绑在一起的元素之间也有顺序之分（内部排列），故最后的安排方法数是两个排列数的乘积。
举例：一家三口去电影院看电影，电影院一排有8个座位，这一家三口要求坐一起，则所有可能的安排方法数为3！×6！＝6×720＝4320种。
(2) 隔板法
隔板法是指把一列元素按一定要求分组的一类方法，它计算分组的方法数，一般是通过在元素的间隙中用相同的隔板来分组，有n个元素（n－1个空），要分m组（需m－1个隔板），那么就有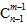
种分组方法。
举例：现有10个小朋友玩游戏，现要将他们分成三组，每组至少要有一个小朋友，则所有可能的分组方法数为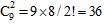
种。
(3) 插空法
插空法和隔板法类似，但还是有所差别，它是求在n个已经排好顺序的队列中再插入m个元素的方法数。对于这类问题，因为插入一个元素就会多出一个空，我们一般按“逐次插入”原则进行求解。
举例：你和小张去火车站买票，只有一个售票窗口，而且前面已经有6个人在排队买票，那么所有可能的插空方法数（不考虑社会秩序）为7×8＝56种。
1．两原理：加法原理和乘法原理
加法原理是一种分类的思想，基本关系是：总个数＝每一类的个数之和。
乘法原理是一种分步的思想，基本关系是：总个数＝每一步的个数之积。
举例：从A地去B地，可选的交通工具有火车、汽车、飞机、轮船，且它们的班次数分别有4、5、2、1个，那么从A地去B地总共的方法数为4＋5＋2＋1＝12种（加法原理——分类）；如果从A地去B地必须中转C地，且从A地去C地有3种交通工具可选，从C地去B地有4种交通工具可选，那么从A地去B地总共的方法数为3×4＝12种（乘法原理——分步）。
2．两计算：排列数和组合数计算
排列讲究先后顺序，用乘法原理可以理解它，其计算式为：
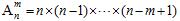。上面是非封闭区间的排列公式，如果是封闭区间（如圆圈），那么还要再除以m（想想为什么？）。
组合不讲究先后顺序，其计算式为：
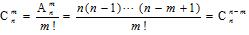。举例：
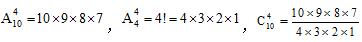
3．两思想：分类讨论思想和互补思想
分类讨论思想是排列组合问题中的基本思想，很多问题都需要分类讨论，分类要找准角度，思维要严谨，做到不重不漏。
互补思想是一种重要的思想，它适用的一般情况是“整体＝一部分＋另一部分”，而问题是求“一部分”，那么我们通过求解“整体”和“另一部分”来间接求出问题。这种思想在前面的几何问题和容斥问题当中已有体现。
4．三方法：捆绑法、隔板法和插空法
这三种方法是排列组合问题中的经典方法，我们在高中数学的时候学习过，现重温一下。
(1) 捆绑法
捆绑法是指一些有特殊要求的元素需要安排在一起，那么我们先将这些元素“捆绑”在一起视为一个元素，参与其他元素的排列（外部排列），因捆绑在一起的元素之间也有顺序之分（内部排列），故最后的安排方法数是两个排列数的乘积。
举例：一家三口去电影院看电影，电影院一排有8个座位，这一家三口要求坐一起，则所有可能的安排方法数为3！×6！＝6×720＝4320种。
(2) 隔板法
隔板法是指把一列元素按一定要求分组的一类方法，它计算分组的方法数，一般是通过在元素的间隙中用相同的隔板来分组，有n个元素（n－1个空），要分m组（需m－1个隔板），那么就有
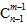种分组方法。举例：现有10个小朋友玩游戏，现要将他们分成三组，每组至少要有一个小朋友，则所有可能的分组方法数为
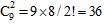种。(3) 插空法
插空法和隔板法类似，但还是有所差别，它是求在n个已经排好顺序的队列中再插入m个元素的方法数。对于这类问题，因为插入一个元素就会多出一个空，我们一般按“逐次插入”原则进行求解。
举例：你和小张去火车站买票，只有一个售票窗口，而且前面已经有6个人在排队买票，那么所有可能的插空方法数（不考虑社会秩序）为7×8＝56种。
责编:一佳教育
